Logical reasoning is key in argumentation, but many miss out on ancient tools. The Square of Opposition, created by Aristotle, is a vital tool for analyzing statements. This piece looks at how this old structure helps in debates, education, and making decisions.
From its start in Aristotle’s philosophy to today, the Square of Opposition connects old wisdom with new challenges.
Preparing for the UGC NET exam can be a daunting task, but with the right resources, candidates can navigate the process effectively. Websites like MyJRF provide a comprehensive platform for aspiring educators, offering specialized guidance for UGC NET Paper 2 preparation and essential tips for acing UGC NET Paper 1. Additionally, understanding the revised syllabus provided by UGC is crucial for a targeted study approach. For official announcements and updates, candidates should regularly visit the UGC NET NTA portal, while the UGC’s job section and the main UGC website are invaluable for post-exam opportunities and academic resources. With these tools, candidates can maximize their preparation and set themselves up for success. Preparing for Paper 1 and UGC NET Paper 2 Education requires a strategic approach with quality resources. UGC NET Education aspirants can access structured video lectures that cover essential concepts comprehensively. For an in-depth understanding, check out teaching aptitude videos and research aptitude guidance to strengthen your foundation. Additionally, higher education system topics and communication skills preparation are crucial for scoring high. Explore logical reasoning tutorials and mathematical reasoning lectures for better problem-solving skills. Enhance your exam strategy with people, development & environment lessons and ICT in education modules. For previous year papers and practice sessions, explore mock test videos and exam strategy tips. Stay ahead in your preparation with teaching methodology insights and subscribe to Educators Plus for expert guidance.
Key Takeaways
- The Square of Opposition visually represents relationships between logical propositions.
- It enhances argumentation by clarifying contradictions and equivalences.
- Aristotle’s framework persists in legal, academic, and everyday reasoning.
- Modern applications include resolving ambiguities in digital communication.
- Understanding the Square improves critical thinking across disciplines.
Understanding Logical Reasoning
Logical reasoning is about using structured thought to check arguments and solve problems. It’s about applying deductive logic and analytical reasoning. This ensures conclusions match the evidence and premises. It’s a key skill that connects abstract ideas with real-world decisions.
Aristotle said, “The educated mind does not accept the impossible,” showing logic’s role in finding truth. This idea is important today, from court debates to scientific studies.
What is Logical Reasoning?
Logical reasoning checks statements for truth. It includes:
- Deductive Logic: Draws conclusions from given facts (e.g., “All A are B. X is A. So, X is B.”)
- Analytical Reasoning: Breaks down information to find patterns (e.g., spotting errors in data-based arguments)
Why is Logical Reasoning Important?
It’s vital in many areas:
- Philosophy: Makes sure arguments follow rules
- Science: Checks hypotheses through tests
- Everyday life: Helps avoid biases in our choices
Common Applications of Logical Reasoning
Many fields use logical methods, including:
| Domain | Implementation |
|---|---|
| Law | Checking if witness statements match |
| Computer Science | Creating algorithms with logical steps |
| Medicine | Diagnosing by analyzing symptoms |
Learning these skills helps people deal with uncertainty. It lets them make decisions based on solid evidence in work and life.
The Fundamentals of the Square of Opposition
The Square of Opposition is key in classical logic. It helps us see how different statements relate to each other. Aristotle and later scholars like Boethius made it a core part of logical reasoning and critical thinking. We’ll explore its structure, parts, and why it’s important today.
Introduction to the Square of Opposition
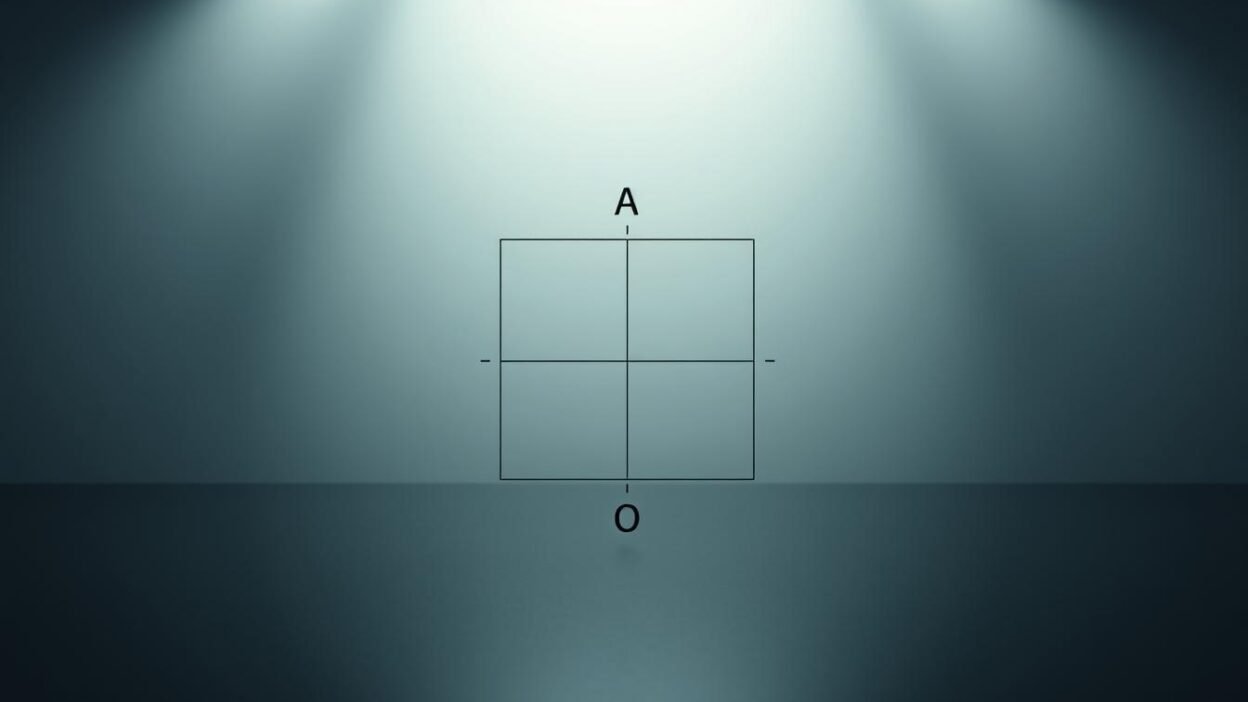
Aristotle started this system in ancient Greece. He divided statements into four types: universal affirmative (A), “All S are P”), universal negative (E, “No S are P”), particular affirmative (I, “Some S are P”), and particular negative (O, “Some S are not P”). Later, medieval scholars turned these into a geometric square. This square helps us understand arguments and spot mistakes.
Structure and Components of the Square
The Square is based on four propositions (A, E, I, O) arranged in a diamond shape. It shows how these statements relate to each other:
| Proposition | Form | Key Relationships |
|---|---|---|
| A (Universal Affirmative) | All X are Y | Contradicts O; Contraries with E |
| E (Universal Negative) | No X are Y | Contradicts I; Contraries with A |
| I (Particular Affirmative) | Some X are Y | Subcontraries with O; Subaltern of A |
| O (Particular Negative) | Some X are not Y | Subcontraries with I; Subaltern of E |
Importance in Logical Analysis
Learning about these relationships improves critical thinking. For example, if “All humans are mortal” (A) is true, it means “Some humans are not mortal” (O) is false. This shows how statements can contradict each other. It’s a skill used in law, school, and everyday life.
Types of Propositions in the Square of Opposition
The Square of Opposition sorts logical statements into four main groups. These groups are the base of deductive logic. They help us solve problems clearly by showing how statements connect.
Each type shows how different categories relate. This helps us analyze arguments in a systematic way.
Universal Affirmative (A Proposition)
Universal Affirmatives say that everything is included: All S are P. For instance, Every prime number is odd is a universal truth. This kind of statement is key for clear conclusions without doubt.
- Form: All S are P
- Example: “All humans are mortal”
- Use: Validates universal truths to eliminate contradictions in reasoning
Universal Negative (E Proposition)
Universal Negatives say nothing is connected: No S are P. For example, No squares are circles sets clear boundaries. These statements help avoid too broad generalizations.
- Form: No S are P
- Example: “No reptiles are mammals”
- Impact: Sharpens logical precision by identifying categorical exclusions
Particular Affirmative (I Proposition)
Particular Affirmatives say some things are included: Some S are P. For example, Some metals are magnetic shows variety. This type adds flexibility to logic while keeping it strict.
- Form: Some S are P
- Example: “Some plants are edible”
- Application: Addresses real-world ambiguity in problem-solving scenarios
Particular Negative (O Proposition)
Particular Negatives say some things are not included: Some S are not P. For example, Some birds cannot fly shows exceptions. These statements are key for detailed analysis.
- Form: Some S are not P
- Example: “Some vehicles are not cars”
- Importance: Identifies limitations in assumptions to strengthen logical conclusions
Contradictories, Contraries, and Subcontraries
Understanding the Square of Opposition is key. It involves three main relationships: contradictories, contraries, and subcontraries. These are the heart of argumentation and analytical reasoning. They help us see how ideas fit together in logical systems.
Defining Contradictories
Contradictories are pairs of statements where one must be true and the other false. For example, “All birds can fly” and “Some birds cannot fly” can’t both be true. This is important in law and philosophy to spot false claims.
Aristotle’s logic shows that when two statements cancel each other out, they stand at opposite ends of truth.
Understanding Contraries
Contraries are statements that can’t both be true but might both be false. Think of “All apples are red” and “No apples are red.” If apples come in other colors, both statements are wrong. This helps us avoid making quick judgments.
Contraries show us extremes, like “Life is meaningless” versus “Life has absolute purpose.”
Exploring Subcontraries
Subcontraries are statements that can both be true but can’t both be false. For instance, “Some books are thrilling” and “Some books are boring” can both be true. This is important in science, where partial truths lead to bigger discoveries.
Subcontraries teach us to look for common ground in debates.
Applications of the Square of Opposition
The Square of Opposition is more than just a tool for logic. It helps in education and real-life situations. It connects theory with practice, improving our thinking and analysis.
Teaching Logical Reasoning
Teachers around the world use the Square in their lessons. It helps break down complex ideas into simple parts. Students learn to understand how different statements work together.
By studying the Square, students learn the basics of logical thinking. This prepares them for more complex tasks later on.
Enhancinging Critical Thinking Skills
Working with the Square improves critical thinking. It teaches students to check if statements are true. For example, comparing a universal affirmative with a particular negative helps spot flaws.
This skill is useful in many areas. It helps evaluate news, research, and even daily choices more accurately.
Role in Philosophy and Debate
Debaters and philosophers use the Square to build strong arguments. It helps them find and counter opposing views. This makes their arguments stronger and more solid.
In philosophy classes, the Square sheds light on old debates. It shows its value in understanding and solving complex issues.
Historical Context of the Square of Opposition
The Square of Opposition was a key part of ancient logic. It started in ancient Greek philosophy, where thinkers organized categorical statements. This method helped shape debates in big ideas like metaphysics and how we know things.
Origin in Ancient Philosophy
Greek philosophers, like Aristotle, first thought about how statements relate. In De Interpretatione, Aristotle talked about the differences between all and some statements. His work on how terms connect has influenced us for centuries.
Contributions of Aristotle
- Defined four proposition types: universal affirmative (A), universal negative (E), particular affirmative (I), particular negative (O)
- Established contradictory relationships between A and O, E and I propositions
- Used syllogistic logic to demonstrate how propositions interact
Evolution Through the Ages
Medieval scholars like Boethius built on Aristotle’s ideas, using them in theological debates. Later, modern logicians fixed problems with empty terms. Today, we use digital tools to show these old ideas in new ways.
Logical Fallacies and the Square of Opposition
The Square of Opposition helps spot logical fallacies by showing how statements relate. It’s based on deductive logic, making it a powerful tool for analyzing arguments. To use it well, you need strong critical thinking skills.
Common Logical Fallacies
Knowing common fallacies is key to understanding logical analysis. Here are a few examples:
- Hasty generalization: Making broad claims based on a few examples
- False equivalence: Saying two things are opposites when they’re not
- Ignoring subcontraries: Missing the fact that some statements can be true together
How the Square Helps Avoid Fallacies
By using the Square, you can check if arguments are valid. For example:
| Proposition Type | Square Relationship | Corrective Insight |
|---|---|---|
| Universal Affirmative | Contradictory to Particular Negative | Prevents unwarranted universal claims |
| Particular Affirmative | Subaltern of Universal Affirmative | Restricts overgeneralization tendencies |
Real-World Examples of Fallacies
In political debates, opponents might say opposing policies are direct opposites. The Square shows this is not always true. In legal cases, using subcontraries wrongly can weaken arguments.
Learning to use the Square improves your critical thinking. It helps you break down arguments and check if conclusions follow logically from the premises.
Visual Aids for Understanding
Visual aids make complex ideas like the Square of Opposition easier to grasp. They help with cognitive processing and solving problems. Diagrams and infographics break down complex logical connections into simple formats. This helps both students and teachers.
Diagrams of the Square of Opposition
Diagrams use shapes to show how ideas relate to each other. Today, they also use colors and layers. For example, they use different colors to show what’s opposite or contradictory. This makes it easier to see how ideas connect.
Infographics for Teaching
Infographics combine text and pictures to help us remember better. Here’s a table that shows why they’re good for learning:
| Aspect | Traditional Diagrams | Modern Infographics |
|---|---|---|
| Structure | Basic lines and symbols | Animated/interactive elements |
| Use in Teaching | Static reference tools | Step-by-step interactive guides |
| Cognitive Impact | Foundation for abstract thinking | Enhanced recall through multimodal learning |
Using Visuals in Presentations
Here are some tips for using visuals in presentations:
- Make important opposition pairs stand out with bold text
- Use flowcharts to show how ideas connect
- Add real-world examples to make it more relatable
These tips help make complex ideas more practical. Tools like Lucidchart or Canva let you create custom visuals for your lessons.
Challenges in Logical Reasoning
Logical reasoning needs to be precise, but it’s not always easy. It faces challenges like unclear statements and applying abstract ideas to real life. Debates today struggle with old limits, like Aristotle’s Square of Opposition not covering all cases.
Common Misunderstandings
People often mix up similar ideas. For instance, contraries and contradictories are not the same. These mistakes come from not really understanding the differences.
Complexity of Logical Structures
Old ways don’t always work in today’s world. Here are some big problems:
| Challenge | Impact |
|---|---|
| Empty Terms | Invalid conclusions from undefined categories |
| Context Dependency | Rules may not apply universally |
Overcoming Logical Limits
- Practice analyzing ambiguous propositions using the Square’s structure
- Apply reasoning skills to real-world dilemmas, such as policy debates
- Engage in peer review to identify fallacies
These steps help improve critical thinking. They make arguments clearer and expose hidden assumptions.
The Square of Opposition in Modern Logic
The Square of Opposition has grown in modern times, facing new challenges in logic. Scholars have made it better, adding new tools for learning. This keeps it useful for many fields.
Adaptations in Contemporary Logic
Today, we focus more on clear logic. George Boole and Gottlob Frege updated the Square for symbolic logic. This makes it easier to understand and use.
Now, digital tools help us see these changes. They make learning and using logic easier.
Digital Tools and Resources
Teachers use Logicly and Stanford’s Intro to Logic on Coursera. These tools help teach logic in a fun way. They include:
- Interactive diagrams for visual learners
- Automated checks for correct logic
- Examples from law and tech
Real-World Applications
Lawyers use the updated Square to analyze cases. Data analysts use it to build theories. In India, IIT Kanpur teaches it in computer science.
This shows how old ideas meet new technology. It helps solve real problems.
Logical Reasoning in Everyday Life
Logical reasoning goes beyond school to guide our daily choices. It helps us make decisions and solve problems. It’s all about using decision-making and problem-solving skills in real life.
Decision Making and Problem-Solving
Good decision-making starts with careful analysis. Think about solving a work issue or picking a financial plan. Here’s how to do it:
- First, figure out the main problem with Socratic questioning.
- Then, weigh the pros and cons of each option.
- Choose based on facts, not feelings.
Analyzing News and Information
Being news savvy means critical thinking. Use logical methods to:
- Check if sources are biased or wrong.
- Break down arguments into premises and conclusions.
- Ignore fallacies like personal attacks.
Enhancing Personal Relationships
Improving relationships means talking in a structured way. Here’s how logical reasoning helps in different areas:
| Scenario | Logical Strategy |
|---|---|
| Family disagreements | Use contradiction analysis to clear up differences |
| Work negotiations | Apply syllogistic reasoning for fair deals |
| Friendship conflicts | Employ subcontraries to find shared interests |
These strategies turn complex ideas into useful tools for everyday life. Mastering logical structures brings clarity to both personal and professional areas.
Cross-Cultural Perspectives on Logical Reasoning
Logical reasoning is not just for one place; it’s a global idea. But, how we see it changes with culture. This part looks at how ideas like the Square of Opposition are seen in different cultures.
Logical Traditions in India
In India, philosophy led to systems like Nyaya and Navya-Nyaya. These focus on careful thinking and checking facts. They match up with today’s ways of reasoning.
Anumana (inference) is like deductive reasoning in Western logic. It shows how ancient Indian thought is connected to modern ideas.
Comparing Eastern and Western Logic
| Aspect | Eastern Traditions | Western Traditions |
|---|---|---|
| Focus | Metaphysical inquiry | Formal structures |
| Key Figures | Aksapada Gautama | Aristotle |
| Modern Relevance | Integrating intuition | Algorithmic applications |
The Global Relevance of the Square
Today, teachers use the Square of Opposition to teach critical thinking. A 2023 UNESCO report shows how it helps students understand different ideas. Now, places like Coursera teach logic in a way that mixes old and new ideas.
“Cultural diversity in logic enriches our analytical reasoning capabilities,” notes Dr. Priya Mehta, Stanford logic scholar.
Learning about different ways of thinking helps us solve big problems. It shows how ideas from around the world can help us think better together.
Teaching Logical Reasoning Effectively
Teaching logical reasoning well mixes old and new methods. Teachers should focus on critical thinking exercises that fit the Square of Opposition. They also need to meet different learning needs. This part shares tips to improve deductive logic and keep students interested.
Effective Teaching Strategies
- Use deductive logic drills to break down syllogisms into manageable steps.
- Incorporate visual aids like the Square of Opposition diagram to clarify proposition relationships.
- Encourage peer-led debates to apply logical reasoning principles in real-time discussions.
Resources for Educators
Teachers can find great resources like Logic Academy or Critical Thinking Hub for lesson plans. Digital tools, such as interactive truth tables and AI-driven logic simulators, offer fun practice. Academic journals like Journal of Logic Education share tested teaching methods.
Engaging Students in Logical Thinking
“Students grasp abstract concepts best through relatable scenarios,” notes Dr. Priya Mehta, logic education specialist. “Linking syllogisms to everyday decision-making bridges theory and practice.”
Use real-life examples like ethical dilemmas or legal arguments to make critical thinking relevant. Apps like Logic Quest make learning logic fun and competitive. Use Venn diagrams and truth tables for regular checks to see how students are doing.
Further Resources and Readings
Improving your logical reasoning skills needs the right materials. These should boost your problem-solving and argumentation. Here are key resources for mastering analytical reasoning:
Recommended Books on Logical Reasoning
- “Introduction to Logic” by Irving M. Copi and Carl Cohen: A foundational text explaining deductive and inductive reasoning structures.
- “The Art of Reasoning” by David Kelley: Explores practical applications of logical frameworks in everyday scenarios.
- “Logic: The Laws of Truth” by Nicholas J.J. Smith: Clarifies formal logic systems with real-world examples.
Online Courses and Tutorials
Platforms like Coursera and edX offer structured learning paths:
- Stanford University’s “Introduction to Logic” on Coursera: Covers formal proof techniques and analytical reasoning exercises.
- MIT OpenCourseWare: “Formal Systems and Logical Deduction” modules for advanced learners.
- Khan Academy’s Logic Fundamentals: Free video tutorials on argumentation and syllogism analysis.
Influential Figures in Logic and Reasoning
“The roots of education are bitter, but the fruit is sweet.” — Aristotle
Key contributors to logical theory include:
- Aristotle: Pioneered categorical syllogisms and the Square of Opposition.
- Gotlob Frege: Revolutionized modern logic with symbolic systems.
- Alfred Tarski: Advanced formal semantics and truth definitions.
Conclusion: The Importance of Logical Reasoning
The Square of Opposition is key in logical analysis, linking ancient wisdom with today’s uses. It boosts our reasoning skills by showing how statements relate to each other. This helps us make clearer decisions. As we face tough challenges, this tool keeps shaping how we think in many fields.
Recap of Key Points
This framework sorts statements into universal and particular types. It defines how they relate, like contradiction and contrariety. Its roots in Aristotle’s logic and its use in AI show it’s always important. It helps us spot fallacies and improve our deductive thinking.
Future of Logical Reasoning in Society
AI advancements show the Square’s real-world value. In healthcare, it helps analyze data for better diagnoses. Autonomous systems use it for safe operation. As tech grows, these systems will need structured reasoning to tackle big issues.
Encouragement for Further Study
Learning from the Square improves our critical thinking in school and work. Resources like logic books or online courses can help. Mastering these skills helps us contribute to AI and make informed decisions worldwide.
FAQ
What is the purpose of the square of opposition?
The square of opposition helps us tackle logical challenges. It shows how different kinds of statements relate to each other. This tool is key for understanding logical arguments in both old and new times.
How does logical reasoning relate to problem-solving?
Logical reasoning is vital for solving problems and asking questions. It helps us check facts, draw conclusions, and solve issues in fields like science and philosophy.
What are the main types of propositions found in the square of opposition?
The square of opposition deals with four main types of statements. These are universal affirmatives (A), universal negatives (E), particular affirmatives (I), and particular negatives (O). Knowing these types is essential for solving logical problems.
What are contradictories, contraries, and subcontraries?
Contradictories are statements that can’t both be true or false at the same time. Contraries can’t both be true but can both be false. Subcontraries can both be true but can’t both be false. Knowing these helps in making better arguments.
How can the square of opposition be applied in educational settings?
It’s great for teaching logical thinking and improving debate skills. By using it in school and debate clubs, teachers can help students understand logical structures better.
What historical figures contributed to the development of the square of opposition?
Aristotle is credited with starting the square of opposition in ancient times. Later, Boethius helped evolve these ideas over the centuries. Their work has shaped how we reason today.
How does the square of opposition help identify logical fallacies?
It shows how some logical mistakes happen. By using this tool, we can spot and fix errors in arguments. This helps avoid misleading reasoning.
Why are visual aids important in understanding the square of opposition?
Visual tools like diagrams make complex ideas easier to understand. They help learners see how different parts of the square of opposition relate to each other.
What challenges are commonly faced in logical reasoning?
People often misunderstand logical concepts and find the structures complex. To overcome these, we need to think critically and improve our reasoning skills.
How has the square of opposition evolved with modern logic?
Today, we use digital tools to teach logical thinking. These new methods help apply the square of opposition in school and real life, showing its ongoing importance.
In what ways can logical reasoning be applied to everyday decision-making?
Logical thinking helps us make better choices and solve problems. It also improves how we analyze information and communicate, leading to stronger relationships.
How do logical reasoning traditions differ across cultures?
Different cultures have their own ways of thinking logically. For example, India and the West have unique approaches. This shows the square of opposition is valuable worldwide for improving reasoning skills.
What are effective strategies for teaching logical reasoning?
Good teaching mixes old methods with new digital tools. Teachers should get students involved in logical thinking. This helps build strong critical thinking and logical skills.
What resources can expand knowledge of logical reasoning?
There are books, online courses, and famous thinkers in logic. These resources help us keep improving our problem-solving and argument skills.