Is a 2,400-year-old tool useful today? The Classical Square of Opposition, from Aristotle, is key to logic and thinking clearly. It shows how statements work together, spotting argument flaws and making our reasoning stronger. By diving into its logical relationships, we learn how old ideas tackle today’s challenges, from school debates to daily decisions.
Why is this old model used today? The Classical Square of Opposition sorts statements into four types, showing their connections. It helps us reason better, whether we’re studying laws or creating AI. This piece will explain its structure, showing its lasting value in many fields.
Preparing for the UGC NET exam can be a daunting task, but with the right resources, candidates can navigate the process effectively. Websites like MyJRF provide a comprehensive platform for aspiring educators, offering specialized guidance for UGC NET Paper 2 preparation and essential tips for acing UGC NET Paper 1. Additionally, understanding the revised syllabus provided by UGC is crucial for a targeted study approach. For official announcements and updates, candidates should regularly visit the UGC NET NTA portal, while the UGC’s job section and the main UGC website are invaluable for post-exam opportunities and academic resources. With these tools, candidates can maximize their preparation and set themselves up for success. Preparing for Paper 1 and UGC NET Paper 2 Education requires a strategic approach with quality resources. UGC NET Education aspirants can access structured video lectures that cover essential concepts comprehensively. For an in-depth understanding, check out teaching aptitude videos and research aptitude guidance to strengthen your foundation. Additionally, higher education system topics and communication skills preparation are crucial for scoring high. Explore logical reasoning tutorials and mathematical reasoning lectures for better problem-solving skills. Enhance your exam strategy with people, development & environment lessons and ICT in education modules. For previous year papers and practice sessions, explore mock test videos and exam strategy tips. Stay ahead in your preparation with teaching methodology insights and subscribe to Educators Plus for expert guidance.
Key Takeaways
- The Square’s four statements form the basis of valid logic analysis.
- Historical origins in Aristotelian philosophy underpin modern logical frameworks.
- Its axioms clarify ambiguities in arguments, reducing misunderstandings.
- Applications span from legal reasoning to algorithmic decision trees.
- Mastery enhances both academic rigor and practical problem-solving skills.
Introduction to the Classical Square of Opposition
The Classical Square of Opposition is a key part of Aristotelian logic. It helps us understand categorical propositions. This logical square has been around for a long time, showing how statements like “All S are P” or “No S are P” relate.
Definition and Historical Context
Aristotle created these ideas in his Organon. This work started the Aristotelian logic. Later, medieval scholars made the Square even more important in their debates. Important moments include:
- Aristotle’s original syllogistic system
- Medieval adaptations by thinkers like Peter Abelard
- Modern interpretations in formal logic
Importance in Logic and Philosophy
This logical square is essential for understanding contradictions and implications. It has four corners for different types of statements. As philosopher Immanuel Kant said:
“The Square’s clarity illuminates the interplay of truth-values in categorical logic.”
Now, it’s used in many fields like law, computer science, and AI. It helps people break down complex arguments in a clear way.
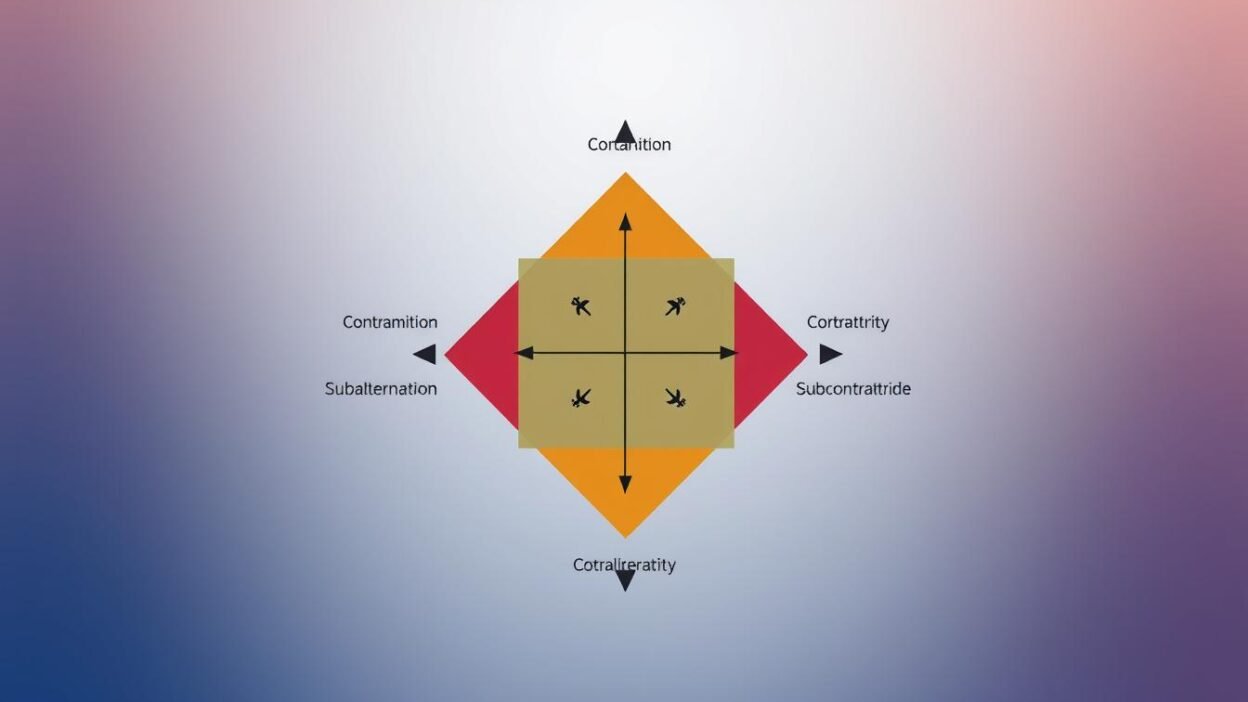
Understanding the Structure of the Square
The classical square of opposition organizes categorical propositions into a structured framework. This logic diagrams visually encodes how statements relate through opposition relations. It enables precise analysis of logical dependencies. Let us dissect its core components.
The Four Types of Statements
At the square’s core are four categorical propositions. Each is defined by quantity (universal/particular) and quality (affirmative/negative):
- Universal Affirmative (A): “All S are P” (e.g., “All humans are mortal”).
- Universal Negative (E): “No S are P” (e.g., “No reptiles are mammals”).
- Particular Affirmative (I): “Some S are P” (e.g., “Some birds can fly”).
- Particular Negative (O): “Some S are not P” (e.g., “Some plants are not edible”).
Relationships Between Statements
The square’s geometry maps six opposition relations. These define how propositions validate or negate one another:
| Relation | Description | Example |
|---|---|---|
| Contradiction | Cannot both be true or false (e.g., A vs. O: “All S are P” vs. “Some S are not P”). | |
| Contrariety | Both cannot be true but can both be false (e.g., A vs. E). | |
| Subcontrariety | Both cannot be false but can both be true (e.g., I vs. O). | |
| Subalternation | If universal is true, particular must also be true (e.g., A → I). | |
| Superalternation | If particular is false, universal must also be false (e.g., I false → A false). | |
| Equivalence | Statements with identical truth values (e.g., A and O contradict; I and E contradict). |
These opposition relations form the square’s logical architecture. They enable systematic analysis of deductive validity. Mastery of this framework clarifies how propositions interact in debates, formal reasoning, and algorithmic logic systems.
The Four Axioms of the Square
The Square of Opposition is based on four categorical propositions in Aristotelian logic. These are Universal Affirmative (A), “All S are P”), Universal Negative (E, “No S are P”), Particular Affirmative (I, “Some S are P”), and Particular Negative (O, “Some S are not P”). Each logical relationships shows how valid a syllogism is. They help us understand truth and how to draw conclusions.
Universal Affirmative (A)
This proposition says “All S are P,” showing total inclusion. It assumes S exists but doesn’t require P to exist. For example, “All mammals are warm-blooded” shows mammals exist but doesn’t require “warm-blooded” to exist. A propositions are key for making universal statements.
Universal Negative (E)
The E proposition (“No S are P”) denies any overlap between S and P. For instance, “No reptiles are mammals.” This strict denial is a core part of Aristotelian logic, opposing the O proposition (“Some S are P”).
Particular Affirmative (I)
The I proposition (“Some S are P”) says both S and P exist. Unlike A, it doesn’t just assume S exists. For example, “Some dogs are pets” shows both dogs and pets exist. This allows for connections between universal and particular statements.
Particular Negative (O)
The O proposition (“Some S are not P”) denies total inclusion. An example is “Some birds are not flightless.” This directly opposes A statements and works with E through contrariety, a key logical relationships in the Square.
These four axioms form a system where each proposition’s form and existence assumptions guide their interactions. Understanding these categorical propositions shows how Aristotelian logic maps out the possibilities of predication and inference.
Contradictory and Contraposed Relations
Understanding opposition relations is key. It shows how statements interact through contradiction and contraposition. These logical relationships help us see the difference between truth and lies.
Definition and Explanation
Contradictory statements are where one is true and the other is false. They are different from contrary statements, which can’t both be true but might both be false. For example, “All S are P” and “Some S are not P” are contradictory pairs.
Contraposition changes a statement by switching its terms but keeps it true. For example, “All S are P” becomes “All non-P are non-S.”
- Contradiction: A-O and E-I pairs (e.g., “All birds fly” vs. “Some birds do not fly”).
- Contraposition: A statement and its contrapositive maintain truth-value equivalence (e.g., “No mammals are reptiles” ↔ “No reptiles are mammals”).
Examples of Contradictory Relationships
“Contradiction is the ultimate test of logical opposition,” noted Aristotle in Analytics, underscoring their role in refining arguments.
Consider:
- Legal context: “Every contract must be written” contradicts “Some contracts need not be written.”
- Ethical debate: “All ethical decisions prioritize utility” vs. “Some ethical decisions reject utility.”
Knowing these logical relationships makes us better at analyzing arguments. It helps us avoid mistakes and use logic correctly.
Subalternation and Its Implications
The Square of Opposition shows how universal and particular statements work together in categorical syllogisms. This is key to understanding logical relationships. It helps us see how conclusions are drawn from given information.
Understanding Subalternation
Subalternation links universal statements (A/E) to their specific counterparts (I/O) by shared quality. For example, if “All S are P” (A-type) is true, then “Some S are P” (I-type) must also be true. But, saying “Some S are P” doesn’t prove a universal statement. This shows a basic rule in logic: we can move from general to specific but not the other way.
“Subalternation reflects the inherent structure of reality,” noted Aristotle in Organon, highlighting its role in linking abstract ideas to real-world observations.
The Role in Logical Deduction
Subalternation makes it possible to make quick, important deductions in syllogisms. Here’s how it works:
- A universal affirmative (A) supports its subaltern particular (I): All roses are flowers → Some roses are flowers.
- A universal negative (E) supports its subaltern particular (O): No birds are mammals → Some birds are not mammals.
| Statement Type | Example | Subaltern | Implication |
|---|---|---|---|
| Universal Affirmative (A) | All humans are mortal | I: Some humans are mortal | Guarantees existence of instances |
| Universal Negative (E) | No reptiles are warm-blooded | O: Some reptiles are not warm-blooded | Validates specific denials |
Today, some logicians question subalternation’s assumptions. But, it’s essential for studying categorical syllogisms. Knowing about subalternation improves our ability to reason in law, science, and computer logic.
The Square and Modern Logic
The Classical Square of Opposition has deep roots in ancient philosophy. Yet, it remains a key part of logic today. Its logical relationships offer insights that guide both computational reasoning and theoretical progress.
Applications in Contemporary Logical Analysis
Modern logicians have updated the Classical Square to tackle new challenges. They’ve introduced the logical hexagon and octagon, expanding on Aristotle’s work. These new models address the Square’s limitations, keeping its core ideas while adding new features.
Predicate logic, for example, uses the Square to study quantifiers in formal proofs. This shows how the Square’s ideas are vital in academic discussions.
Relevance in Computer Science and AI
The Classical Square of Opposition plays a big role in computer science and AI. It’s used in three main ways:
- Knowledge Representation: The Square helps organize data in semantic web technologies. It makes data easier for machines to process.
- Expert Systems: AI uses the Square to create decision trees. This ensures that AI systems make consistent decisions.
- Formal Verification: The Square helps check if code is correct. It tests different scenarios to ensure code works as expected.
Programming languages like Prolog use the Square’s logic for solving problems. AI models apply oppositional reasoning in tasks like understanding natural language. This blend of ancient logic and modern tech shows the Square’s lasting value in solving today’s problems.
Common Misconceptions
Understanding the logical square needs careful attention to avoid common mistakes. These errors often come from simplifying Aristotelian logic too much. This can lead to wrong conclusions in debates and academic papers.
Misinterpretations of the Square’s Functions
There are three main mistakes:
- Confusing contrary vs. contradictory relations: Contrary statements (like “All S are P” vs. “No S are P”) can both be wrong. But contradictories can’t.
- Assuming symmetrical relationships: The square is not symmetrical. This means how statements interact depends on their position and type.
- Ignoring existential import: Universal statements, like “All men are mortal,” can be interpreted differently. This affects how we understand categorical syllogisms.
Clarifying Logical Relationships
“The square’s rigor demands strict adherence to its axioms,” noted scholars addressing modern misapplications.
Existential import is a big topic of debate. Aristotle’s original ideas didn’t assume universal statements prove existence. Yet, many today mix these ideas up. For example, saying “All unicorns are mythical” follows Aristotelian logic without saying unicorns exist. This difference is key for using categorical syllogisms correctly. Making these points clear helps in legal arguments, AI, and academic studies.
Practical Applications
The Classical Square of Opposition turns complex logical relationships into practical tools. It helps solve real-world problems. It makes personal choices and academic studies clearer by showing contradictions and proving deductions right.
Use in Daily Decision-Making
Its framework is useful in everyday life:
- Decoding political rhetoric: Spot universal claims (“All policies benefit everyone”) from unsupported particular statements (“Some groups may be excluded”).
- Evaluating ethical dilemmas: Map opposing options onto the Square to find logically inconsistent choices.
- Resolving disputes: Use oppositional axioms to find fallacies in conflicting viewpoints.
Application in Academic Research
In scholarly contexts, it adds analytical rigor:
- Philosophers analyze ethical theories by testing their categorical consistency
- Linguists model language ambiguities through its four-statement structure
- Computer scientists implement its logic in AI algorithms for automated inference validation
“The Square’s systematic approach ensures no logical possibility goes unexamined,” states the 2023 Oxford Handbook of Logic, highlighting its role in maintaining academic integrity.
Whether checking news headlines or designing research methods, the Square’s framework helps dissect logic in everyday and scholarly discourse.
Conclusion: Mastering Logical Relationships
The Classical Square of Opposition is a timeless tool for understanding logical connections. It breaks down categorical propositions into parts. This helps us deal with unclear and precise ideas in our thinking.
It’s not just a piece of history. It’s a flexible tool for today’s challenges too.
Recap of Core Principles
The Square is built on four key statements: universal affirmative (A), universal negative (E), particular affirmative (I), and particular negative (O). These statements are linked by important oppositions.
These links show how statements can support or contradict each other. This is the heart of syllogistic logic. Today, it’s used in computer science and law, showing its lasting value.
Pathways for Continued Exploration
Studying the Square can lead to deeper understanding. Look into the hexagon of opposition for more complex thinking. Modal logic and computational logic also connect to classical ideas.
Resources like History and Philosophy of Logic and Stanford Encyclopedia of Philosophy offer more to learn. Mastering these systems improves critical thinking. It helps both students and professionals solve complex problems with clarity.
FAQ
What is the Classical Square of Opposition?
The Classical Square of Opposition is a diagram that shows how different kinds of statements relate. It helps us understand the connections between universal and particular statements. This includes things like contradiction, contrariety, subalternation, and equivalence.
How does the Square of Opposition relate to Aristotelian logic?
The Square of Opposition comes from Aristotle’s work on logic. It makes his ideas on syllogisms and statements clearer. This framework has grown over time and is used today.
What are the four types of categorical statements represented in the Square?
The Square shows four kinds of statements:
- A (Universal Affirmative): “All S are P”
- E (Universal Negative): “No S are P”
- I (Particular Affirmative): “Some S are P”
- O (Particular Negative): “Some S are not P”
Each statement has its own logical properties and relationships.
Can you explain the concept of subalternation?
Subalternation is about the relationship between universal and particular statements. If a universal statement is true, like “All S are P”, then the particular statement “Some S are P” must also be true. But the reverse isn’t always true, showing the direction of truth.
How are contradictions and contrapositions defined in the Square?
Contradictions are statements that can’t both be true or both be false (e.g., A and O, E and I). Contraposition changes a statement while keeping its truth, like turning “All S are P” into “All non-P are non-S”. Knowing these is key for logical thinking.
What are common misconceptions about the Square of Opposition?
People often simplify its role or mix up its relationships, like confusing contrary with contradictory. They also miss the fine points of what’s assumed to exist in universal and particular statements.
How can the Classical Square of Opposition be applied in daily decision-making?
The Square helps us spot contradictions in arguments and avoid fallacies. It makes our thinking clearer on social issues, personal choices, and policy debates. By mapping out claims, we can make better decisions.
What relevance does the Square have in modern computer science and AI?
In computer science and AI, the Square helps with logical analysis. It structures proposition relationships, key for knowledge and reasoning. Formal verification and expert systems use the Square’s principles to improve computational thinking.