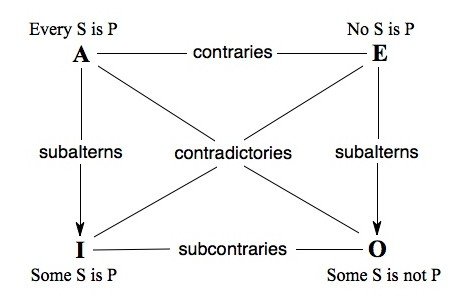
The Classical Square of Opposition is a powerful tool in Aristotelian logic. It visually shows how different statements relate to each other. This ancient diagram still holds relevance in modern logical discourse.
It helps us understand contradictions, contraries, and subalternations. By mastering it, you’ll gain insights into crafting sound arguments. You’ll also learn to spot flaws in reasoning.
The Square of Opposition isn’t just a philosophical relic. It’s a living tool that influences various fields. These include law and computer science.
This simple yet profound concept can transform your critical thinking. It can also enhance your argumentation skills. Let’s explore how it shapes our understanding of logical relationships.
Preparing for the UGC NET exam can be a daunting task, but with the right resources, candidates can navigate the process effectively. Websites like MyJRF provide a comprehensive platform for aspiring educators, offering specialized guidance for UGC NET Paper 2 preparation and essential tips for acing UGC NET Paper 1. Additionally, understanding the revised syllabus provided by UGC is crucial for a targeted study approach. For official announcements and updates, candidates should regularly visit the UGC NET NTA portal, while the UGC’s job section and the main UGC website are invaluable for post-exam opportunities and academic resources. With these tools, candidates can maximize their preparation and set themselves up for success.
Key Takeaways
- The Classical Square of Opposition is a fundamental tool in Aristotelian logic
- It visually represents relationships between different types of statements
- Understanding the square enhances critical thinking and argumentation skills
- The concept remains relevant in modern logical discourse
- Mastery of the square aids in identifying and avoiding logical fallacies
Understanding the Classical Square of Opposition
The Classical Square of Opposition is a key concept in traditional logic. It’s a tool from Aristotelian logic that shows relationships between categorical propositions. Let’s dive into its core, history, and importance in logical thinking.
What is the Classical Square of Opposition?
The Classical Square of Opposition is a visual diagram in traditional logic. It shows logical links between four types of categorical propositions. This concept helps thinkers analyze connections between different statements.
Historical Context
Aristotle, who founded formal logic, created the basis for the Square of Opposition. He did this in his work on categorical syllogisms. Over time, logicians improved his ideas.
They made the Square a key part of traditional logic studies. This process took place over many centuries.
Importance in Logic
The Square of Opposition is vital for logical reasoning. It helps identify contradictions and contraries in arguments. It also shows links between universal and particular statements.
The Square aids in judging the truth of related propositions. It’s useful for building logical arguments effectively.
Learning the Classical Square of Opposition gives logic students a powerful tool. They can analyze arguments and create sound reasoning in many fields. These include philosophy, science, and everyday talks.
| Aspect | Contribution to Logic |
|---|---|
| Visualization | Provides a clear diagram of logical relationships |
| Analysis | Enables systematic examination of propositions |
| Reasoning | Enhances ability to draw valid conclusions |
| Education | Serves as a fundamental teaching tool in logic |
The Four Types of Propositions
Categorical propositions are key in predicate logic. They form the basis of the Classical Square of Opposition. These propositions come in four types, each vital for logical reasoning.
Universal Affirmative
Universal affirmatives make broad claims about entire categories. They follow the form “All A are B.” For example, “All cats are mammals.”
This type states that every member of one group belongs to another. It leaves no room for exceptions.
Universal Negative
Universal negatives state that no members of one group belong to another. They use the structure “No A are B.” An example is “No squares are circles.”
These propositions show a complete split between two categories. They leave no overlap between the groups.
Particular Affirmative
Particular affirmatives claim that some group members have a certain quality. They’re expressed as “Some A are B.” For instance, “Some students are athletes.”
This type allows for partial overlap between categories. It doesn’t specify the exact extent of the overlap.
Particular Negative
Particular negatives state that some group members lack a certain quality. They take the form “Some A are not B.” An example is “Some birds are not flightless.”
These propositions show partial exclusion within a category. They indicate that not all members share a specific trait.
| Proposition Type | Structure | Example |
|---|---|---|
| Universal Affirmative | All A are B | All dogs are animals |
| Universal Negative | No A are B | No humans are immortal |
| Particular Affirmative | Some A are B | Some fruits are sweet |
| Particular Negative | Some A are not B | Some cars are not electric |
These four proposition types are crucial for understanding logical reasoning. They help us grasp the Classical Square of Opposition. Knowing them aids in applying logic to various situations.
Relationships Between Propositions
Traditional logic explores connections between propositions to build sound reasoning. The Classical Square of Opposition shows these logical links. It offers a framework for analyzing and evaluating statements.
Contradictory Relationships
Contradictory propositions can’t be true at the same time. If one is true, the other must be false. This idea is key to developing critical thinking skills.
It also helps in building valid arguments. Understanding contradictions improves our ability to reason logically.
Contrapositive Relationships
Contrapositive statements are logically equivalent. If one is true, its contrapositive must also be true. This principle is crucial in proof techniques and logical reasoning.
Subalternation: A Hierarchy of Truth
Subalternation links universal and particular propositions. It shows that if a universal statement is true, its particular form is also true. This concept helps us draw valid conclusions from general principles.
| Relationship Type | Description | Example |
|---|---|---|
| Contradictory | Opposite truth values | “All cats are black” vs “Some cats are not black” |
| Contrapositive | Logically equivalent | “If it rains, the ground is wet” vs “If the ground is not wet, it did not rain” |
| Subalternation | Hierarchical truth | “All dogs are mammals” implies “Some dogs are mammals” |
Understanding these logical relationships sharpens our ability to analyze arguments. It helps us spot fallacies and build sound reasoning. These skills apply to various fields of study and everyday life.
Visualizing the Square of Opposition
The Classical Square of Opposition helps us understand logical relationships. Visual aids make complex concepts easier to grasp. Let’s explore the diagram’s layout and key components.
Diagram Layout
The Square of Opposition is a square with four corners. Each corner stands for a different type of proposition. This simple layout shows how propositions relate to each other.
Key Components Explained
The four corners of the Square represent:
- Universal Affirmative (A): Top left
- Universal Negative (E): Top right
- Particular Affirmative (I): Bottom left
- Particular Negative (O): Bottom right
The lines connecting these corners show different relationships:
| Relationship | Connection | Meaning |
|---|---|---|
| Contradictory | Diagonal lines | Opposites that can’t both be true or false |
| Contrary | Top horizontal line | Can’t both be true, but can both be false |
| Subcontrary | Bottom horizontal line | Can’t both be false, but can both be true |
| Subalternation | Vertical lines | If universal is true, particular must be true |
The Square of Opposition visually shows relationships between logical statements. It helps us quickly understand these complex concepts. This tool improves our critical thinking and argumentation skills.
Practical Applications in Everyday Reasoning
The Classical Square of Opposition sharpens our minds and improves our thinking. It’s a powerful tool for better communication. This logical framework boosts critical thinking and strengthens arguments.
Critical Thinking Skills
The Square of Opposition enhances our ability to analyze complex ideas. It trains us to spot contradictions and evaluate argument strength. This skill is vital in law, science, and politics.
- Identifying logical relationships between statements
- Recognizing fallacies in arguments
- Evaluating the validity of claims
Enhancing Argumentation Techniques
The Square of Opposition helps build solid arguments. Understanding proposition relationships leads to more persuasive, logical arguments. This is useful in debates, academic writing, and professional presentations.
“The art of argumentation is not about winning debates, but about advancing understanding.”
These principles improve communication and problem-solving in daily life. They guide you to rational conclusions when analyzing news or making decisions.
Logical reasoning skills from the Square of Opposition are valuable in discussions. They help create well-supported arguments in various situations.
Common Misconceptions About the Square
The Classical Square of Opposition helps with critical thinking but often leads to misunderstandings. These can cause logical fallacies and flawed reasoning. Let’s look at some common errors and their solutions.
Misinterpreting Contradictory Statements
People often mix up contrary and contradictory statements. Contradictory statements can’t be true or false simultaneously. “All cats are black” and “Some cats are not black” are contradictory examples.
If one of these statements is true, the other must be false. Understanding this difference is crucial for clear logical thinking.
Overgeneralizing Relationships
Another mistake is forcing all propositions into the square’s four categories. Real-world statements often have nuances that don’t fit perfectly. This can lead to oversimplification and wrong conclusions.
Complex ideas shouldn’t always be squeezed into this framework. It’s important to recognize when the square applies and when it doesn’t.
To avoid these errors, it’s crucial to:
- Carefully analyze each statement before categorizing it
- Consider context and nuance in real-world applications
- Practice identifying true contradictions versus mere contraries
- Remember that the square is a tool, not an absolute rule for all logic
Understanding these misconceptions can improve your critical thinking skills. You’ll use the Classical Square of Opposition more effectively in your reasoning and arguments.
Developing Logical Arguments
Logical reasoning is crucial for building strong arguments. It helps you present ideas clearly and avoid thinking pitfalls. Let’s explore how to structure thoughts and avoid logical fallacies.
Structuring Your Reasoning
Effective argumentation starts with a solid structure. Begin with a clear thesis statement. Then, provide supporting evidence and examples.
This approach creates a logical flow that others can easily follow. It helps strengthen your overall argument.
- State your main point clearly
- Provide evidence to support your claim
- Address potential counterarguments
- Conclude by reinforcing your thesis
Avoiding Logical Fallacies
Logical fallacies can weaken your arguments. These are common errors in reasoning that lead to incorrect conclusions. Recognizing these pitfalls helps strengthen your logical reasoning skills.
| Fallacy | Description | Example |
|---|---|---|
| Ad Hominem | Attacking the person instead of the argument | “You’re wrong because you’re not an expert.” |
| Straw Man | Misrepresenting an opponent’s argument | “You want to ban all cars? That’s crazy!” |
| False Dichotomy | Presenting only two options when more exist | “You’re either with us or against us.” |
Good argument structure and avoiding fallacies lead to stronger reasoning skills. Practice these techniques to improve your critical thinking. You’ll also enhance your communication abilities.
Teaching the Classical Square of Opposition
Logic education thrives when teachers use effective methods to introduce complex concepts. The Classical Square of Opposition can be challenging to teach. Let’s explore ways to make this topic engaging and easy to understand.
Methods for Educators
Teachers can improve logic education by using different teaching techniques. Visual aids are key in explaining the Square of Opposition. Interactive diagrams help students understand relationships between propositions better.
Group discussions help students think critically. Teachers can use real-life examples to show how the Square applies to everyday situations. This makes abstract ideas more concrete for students.
Engaging Classroom Activities
Hands-on activities boost learning and improve critical thinking. Here are some fun exercises for teaching the Classical Square of Opposition:
- Proposition Creation: Students generate their own sets of propositions and map them onto the Square.
- Debate Tournaments: Organize debates where students use the Square to analyze and construct arguments.
- Logic Puzzles: Design puzzles that require students to apply the principles of the Square to solve them.
| Activity | Skills Developed | Time Required |
|---|---|---|
| Proposition Creation | Analytical Thinking | 30 minutes |
| Debate Tournaments | Argumentation | 60 minutes |
| Logic Puzzles | Problem-Solving | 45 minutes |
These teaching methods and activities create an exciting learning environment. They help students understand the Classical Square of Opposition better. Students also improve their logical reasoning skills through these exercises.
Advanced Concepts Related to the Square
Modern logic has expanded the Classical Square of Opposition. It now applies to predicate logic and other frameworks. This growth has deepened our grasp of logical relationships and argumentation.
Modern Extensions of the Square
The Square of Opposition has new dimensions in predicate logic. It now covers quantified statements, enabling more detailed analysis of complex ideas. This expansion has sparked advanced logical systems for intricate real-world scenarios.
Integrating with Other Logical Frameworks
Combining the Square with other frameworks has created powerful reasoning tools. Modern logic merges the Square’s principles with modal, fuzzy, and computational logic. This blend improves our ability to model and study complex systems.
| Logical Framework | Integration with Square of Opposition | Application |
|---|---|---|
| Predicate Logic | Extended to quantified statements | Mathematical proofs |
| Modal Logic | Applied to possibility and necessity | Philosophical arguments |
| Fuzzy Logic | Used for degrees of truth | Artificial intelligence |
These advances highlight the Square of Opposition’s lasting importance in logical thinking. Its core ideas continue to influence reasoning methods. They shape how we approach arguments in both academic and practical settings.
Conclusion: The Enduring Relevance of the Square
The Classical Square of Opposition is vital for logical reasoning. It helps us grasp relationships between different statement types. This tool sharpens our critical thinking skills and improves argument analysis.
Summary of Key Takeaways
The Square of Opposition categorizes propositions into four types. These are universal affirmative, universal negative, particular affirmative, and particular negative.
These categories help us understand contradictory, contrary, and subalternate relationships. This knowledge is crucial for building strong arguments and identifying flaws in reasoning.
Final Thoughts on Logical Thought
The Classical Square of Opposition remains relevant in modern times. It’s a foundation for critical thinking in philosophy, law, and science.
Applying these principles enhances our analytical and communication skills. It also helps us make better decisions. The Square is essential for anyone wanting to improve their logical reasoning abilities.
FAQ
What is the Classical Square of Opposition?
The Classical Square of Opposition is a key tool in Aristotelian logic. It shows the links between four types of statements. These are universal and particular affirmatives and negatives. This tool helps us understand logic and build strong arguments.
How does the Classical Square of Opposition enhance critical thinking?
The Classical Square of Opposition boosts critical thinking skills. It offers a framework for studying logical links between statements. This tool helps spot contradictions and build valid arguments. Users can better assess claims and find flaws in reasoning.
What are the four types of propositions in the Classical Square of Opposition?
The Classical Square of Opposition has four proposition types. These are Universal Affirmative (A), Universal Negative (E), Particular Affirmative (I), and Particular Negative (O). Each type represents a different categorical statement. They form the basis of traditional logic.
How can understanding contradictory relationships improve argumentation?
Grasping contradictory relationships helps improve arguments. It allows us to spot statements that can’t be true or false at once. This knowledge helps create stronger premises and avoid logical errors. It also aids in refuting opposing arguments more effectively.
What is subalternation in the context of the Square of Opposition?
Subalternation shows the link between universal and particular propositions. It applies to statements of the same quality, either affirmative or negative. If a universal proposition is true, its particular counterpart must be true too.
How can educators effectively teach the Classical Square of Opposition?
Teachers can use visual aids and interactive tasks to teach the Classical Square of Opposition. Group talks on logical relationships help students grasp the concept. Applying the Square to current events makes learning more engaging.
Practice in building and studying arguments is also useful. These methods help students understand and use these concepts more effectively.
What are some common misconceptions about the Classical Square of Opposition?
People often mistake contradictory statements for merely contrary ones. Some wrongly think the Square applies to all statement types. Others overgeneralize the links between different proposition types. Understanding these errors is key to using the Square correctly.
How has the Classical Square of Opposition evolved in modern logic?
Modern logic has expanded the Classical Square of Opposition. It now fits more complex logical systems. Logicians have created more detailed diagrams, adding modal logic and quantification theory. The basic ideas still matter, but they’re part of wider reasoning frameworks now.
Can the Classical Square of Opposition be applied to everyday reasoning?
The Classical Square of Opposition helps in daily reasoning. It’s useful for analyzing arguments and evaluating news reports. This tool aids in spotting logical flaws and building stronger arguments. It’s valuable in both personal and work situations.
What role does the Classical Square of Opposition play in avoiding logical fallacies?
The Classical Square of Opposition helps prevent logical errors. It shows how different types of statements relate to each other. This knowledge helps avoid invalid conclusions and confused reasoning. It’s crucial for making sound arguments and spotting flaws in others’ logic.